計算數字中 On 的 bits
計算數字中 On 的 bits
本文重點
- Bits 與數字的關係
- 常見 Bits 相關名詞
- 計算 Bits set 的數量
- Brian Kernighan 演算法
在介紹這次演算法前,先介紹一些相關的知識。
Bits
Bit 是「Binary Digit」的縮寫,意思是二進制數位。它是電腦中最基本的數據單位,只能有兩種值:0 或 1。你可以把它想像成一個開關,只有兩個狀態:開或關。
當多個 Bit 組合在一起時,就可以表示更複雜的信息。例如,8 個 Bit 組成一個「Byte」,可以表示從 0 到 255 的整數。這樣的組合讓電腦可以儲存和處理各種不同類型的數據。
看看以下將 10 進位數字轉成 2 進位的範例
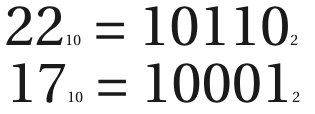
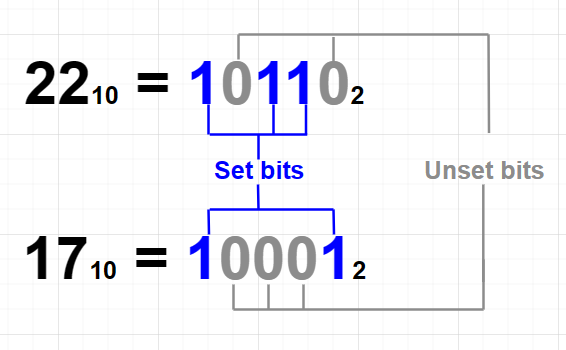
Set and Unset Bit
Set bit : 設為 1 的位元 Unset bit : 設為 0 的位元
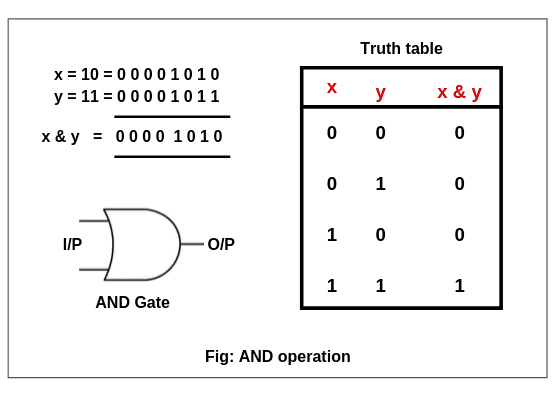
Bitwise AND Operator(&)
當兩個 Bits 都是 1 時回傳 1 否則回傳 0
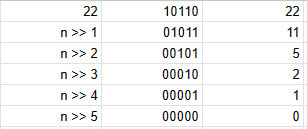
Bitwise Right-Shift Operator
Right shift 的行為就是將現在所有的 Bits 往右移動一定的位數。對於 10 進位來說等於除以 2 的 n 次方。
以上就是本篇演算法會用到的知識;那就進入主題吧。
計算 Bits 中 Set 的數量
這是一個經典題目,解法也有蠻多種的。
Leetcode 191. Number of 1 Bits
Brute Force
最直覺的做法就是歷遍每個 Bit,如果該 Bit 是 1 的話結果就加 1,判斷該 Bit 是否為 1 就是利用 AND Operator,而歷遍就是利用 Right-ShiftOperator。
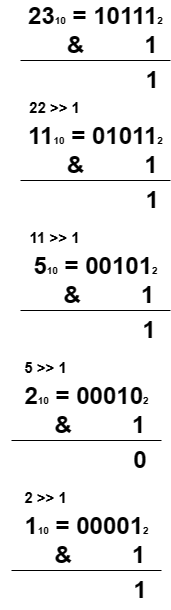
Code Implementation
時間複雜度:O(log(n))。
空間複雜度:O(1)。
n : 數字中全部的 Bit 數量。
public static int BitsCount(int num)
{
var res = 0;
while (num > 0)
{
res += num & 1;
num >>= 1;
}
return res;
}
Brian Kernighan’s algorithm
這個算法的主要思想是通過不斷地利用二進制數 n 和 n-1 進行按位與(AND)運算,每次運算都會消除 n 中最右邊的一位 1。當 n 變為 0 時,表示所有的位 1 都已經被消除,同時計算的次數也就是原始數中包含的位數。

Code Implementation
時間複雜度:O(log(n))。
空間複雜度:O(1)。
n : 數字中 Set 的 Bit 數量。
public static int BitsCount(int num)
{
var res = 0;
while (num > 0)
{
num &= (num - 1);
res++;
}
return res;
}
結論
| Brute Force | Brian Kernighan’s algorithm | |
| 時間複雜度 | O(log(n)) | O(log(n)) |
| 空間複雜度 | O(1) | O(1) |
| n | 數字中全部的 Bit 數量 | 數字中 Set 的 Bit 數量 |
在常見的 Int32 的資料形式中,這兩種演算法並不會有太明顯的差異;但當處理大型數據集時 Brian Kernighan’s algorithm 的優勢就會顯現出來了。